Shortest hyperpath heuristic
|
Overview
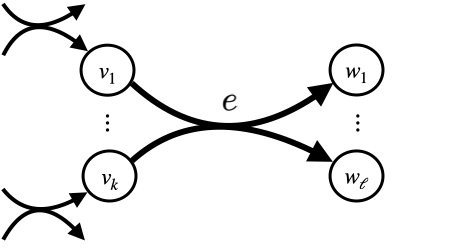
Our fast heuristic is the first available method for the shortest source-sink hyperpath problem in general directed hypergraphs (which is NP-complete), where hyperedges have arbitrary tail and head sets, and the length of a hyperpath is the sum of the weights of its hyperedges. Our heuristic always finds an s,t-hyperpath if one exists and appropriately handles cycles. While the heuristic is not guaranteed to find a shortest s,t-hyperpath in general, our results show it quickly finds a hyperpath that is optimal on over 99% of real-world instances.The heuristic proceeds similarly to Dijkstra's algorithm for finding shortest paths in ordinary graphs, but with several key differences. Our heap is composed of hyperedges e, which are prioritized by the length of the shortest known hyperpath from s to e. Computing the length of this shortest s,e-hyperpath is also NP-complete, so we use a greedy heuristic to compute approximate shortest s,e-hyperpaths.
Source code
The hyperpath heuristic source code is available on GitHub.Videos
|
The following video was presented at WABI 2020 and gives more detailed information on the heuristic:
|
A shorter version was presented at SCS 2021:
|